Two Sum Problem

Two Sum problem is a classic problem. Let us solve this using five different types from brute force to an optimized approach using Hashtable.

Introduction

Two Sum problem is a classic problem and this has been listed first as one of the basic questions one has to solve when prepping for coding interviews. Leetcode, one of the largest tech communities with hundreds of thousands of active users to participate and solve coding problems listed this as the first problem in their curriculum – the Leetcode TwoSum Problem.

Let us discuss the TwoSum algorithm of a given input. This is one of the most popular questions asked in coding interviews.

Companies that have asked this in their coding interview are Facebook, Amazon, Apple, Netflix, Google, Microsoft, Adobe, and many more top tech companies.

Problem Statement

In the TwoSum Problem given an array of integers, nums and an integer, return the two numbers such that they add up to the target. You may assume that each input would have exactly one solution, and you may not use the same element twice. You can return the answer in order.

Example 01:

Input: nums = [2, 7, 11, 15], target = 9

Output: [2, 7] // (because nums[0] + nums[1] == 9, we return [2, 7])

Example 02:

Input: nums = [3, 2, 4], target = 6

Output: [2, 4]

Example 03:

Input: nums = [3, 3], target = 6

Output: [3, 3]

Thought Process

First way

Let us consider the array as {3, 5, -4, 8, 11, 1, -1, 6}, and target = 10.

Considering unique integers, you can use the Set interface or Map in Java.

Let X, Y below the two numbers, the question clearly states that two numbers add up to the target. We can represent this mathematically by –

X + Y = 10   =>   Y = ( 10 - X )

So, when iterating the elements you get X value and check if ( 10 - X) which is Y present in the hashtable, isn’t that easy to find? also, this is a constant lookup time.

Time complexity: O(n) is the worst case, where we need to iterate all the elements.

Space complexity is O(n), storing elements is HashTable.

Second way: Any Optimizations to above?

Can we solve this in a more optimal, with no extra space?

Yes, first we sort the entire array, and then we use the two pointers left, right to find the target sum.

• Sorting takes O(N log N) and finding the sum takes O(n).
• Overall the time it takes is O(N log N) and space O(1).

We look at this two-pointer approach at the last, let us see some of the options we can solve this.

If you want to get good with algorithms and problem-solving and improve your understanding of problems and ways to handle them, then you need to see how solutions are implemented in all possible ways.

Solution

Approach#1: Brute Force

The brute force approach is simple, loop through each element x and find another value that equals (target - x).

import java.util.Arrays;

public class TwoSum {
  public static void main(String[] args) {
    int[] input = {2, 7, 11, 15};
    int targetSum = 18;
    System.out.println(Arrays.toString(twoSum(input, targetSum)));
  }

  public static int[] twoSum(int[] nums, int targetSum) {
    for (int i = 0; i < nums.length; i++) {
      for (int j = i + 1; j < nums.length; j++) {
        if (nums[j] == targetSum - nums[i]) {
          return new int[]{i, j};
        }
      }
    }
    throw new IllegalArgumentException("No two sum solution");
  }
}

Complexity Analysis

Time complexity: O( n ^ 2 ), for each element, we try to find its complement by looping through the rest of the array which takes O(n) time. Therefore, the time complexity is O( n ^ 2 ), where n is the length of the elements present in the array.

Space complexity: O(1), as no extra space is utilized.

Approach#2: Two-Pass HashTable

We need a more efficient way to check if the complement exists in the array to improve our run time complexity.

If the complement exists, we need to look up its index. What is the best way to maintain a mapping of each element in the array to its index?

We reduce the lookup time from O(n) to O(1) by trading space for speed. A hash table is built exactly for this purpose, it supports fast lookup in the next constant time.

I say “near” because a look-up could degenerate to O(n) time if a collision occurred. But look up in hash table should be amortized O(1) time as long as the hash function was chosen carefully.

A simple implementation uses two iterations. In the first iteration, we add each element’s value and its index to the table.

Then, in the second iteration, we check if each element’s complement(target - nums[i]) exists in the table. Beware that the complement must not be nums[i] itself!

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;

public class TwoSum {
  public static void main(String[] args) {
    int[] input = {2, 7, 11, 15};
    int targetSum = 18;
    System.out.println(Arrays.toString(twoSum(input, targetSum)));
  }

  public static int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();

    for (int i = 0; i < nums.length; i++) {
      map.put(nums[i], i);
    }

    for (int i = 0; i < nums.length; i++) {
      int complement = target - nums[i];
      if (map.containsKey(complement) && map.get(complement) != i) {
        return new int[]{i, map.get(complement)};
      }
    }
    
    throw new IllegalArgumentException("No two sum solution");
  }
}

Complexity Analysis

Time complexity: O(n) We traverse the list containing n elements exactly twice. Since the hash table reduces the look-up time to O(1), the time complexity is O(n).

Space complexity: O(n) The extra space required depends on the number of items stored in the hash table, which stores exactly n elements.

Approach#3: One-Pass HashTable

It turns out we can do it in one pass. While we iterate and insert elements into the table, we also check if the current element’s complement already exists in the table. If it exists, we have found a solution and returned it immediately.

import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;

public class TwoSum {
  public static void main(String[] args) {
    int[] input = {2, 7, 11, 15};
    int targetSum = 18;
    System.out.println(Arrays.toString(twoSum(input, targetSum)));
  }

  public static int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();

    for (int i = 0; i < nums.length; i++) {
      int potentialDifference = target - nums[i];
      if (map.containsKey(potentialDifference)) {
        return new int[]{map.get(potentialDifference), i};
      }
      map.put(nums[i], i);
    }
    throw new IllegalArgumentException("No two sum solution");
  }
}

So, let’s see how we can achieve the same using the Set interface.

import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;

public class TwoSum {
  public static void main(String[] args) {
    int[] input = {2, 7, 11, 15};
    int targetSum = 18;
    System.out.println(Arrays.toString(twoSum(input, targetSum)));
  }

  public static int[] twoSum(int[] array, int targetSum) {
    Set<Integer> set = new HashSet<>();

    for (int num : array) {
      int potentialDiff = targetSum - num;
      if (set.contains(potentialDiff)) {
        return new int[]{potentialDiff, num};
      }
      set.add(num);
    }
    // Write your code here.
    return new int[0];
  }
}

Complexity Analysis

Time complexity: O(n) We traverse the list containing n elements only ones, each lookup in the table only costs O(1) time.

Space complexity: O(n) The extra space required depends on the number of items stored in the table, which stores at most n elements.

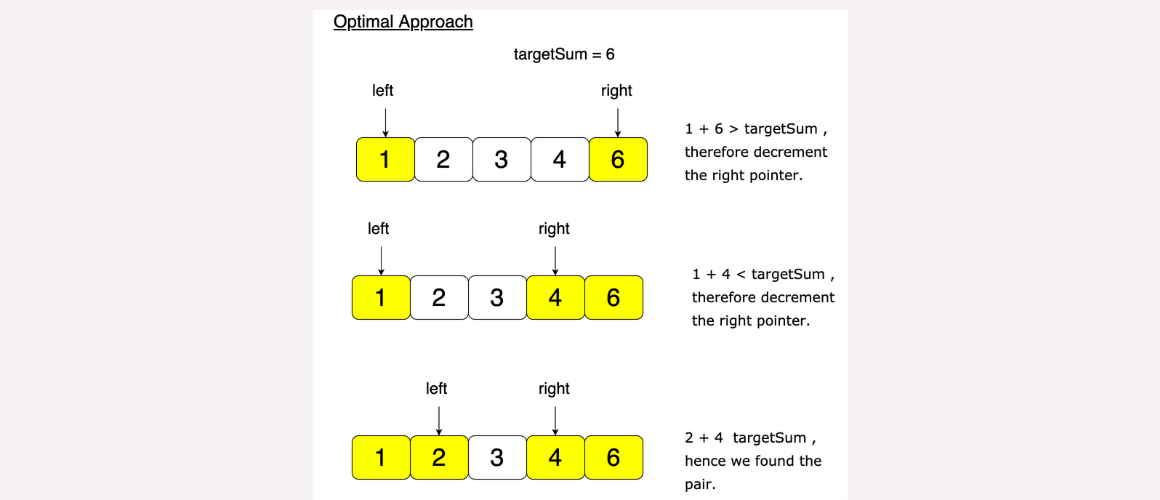
Approach#4: Two Pointer

First, sort the array and then use the two-pointer left, right and iterate them over the array.

import java.util.Arrays;

public class TwoSum {
  public static void main(String[] args) {
    int[] input = {2, 7, 11, 15};
    int targetSum = 18;
    System.out.println(Arrays.toString(twoSum(input, targetSum)));
  }

  public static int[] twoSum(int[] array, int targetSum) {
    Arrays.sort(array);

    int left = 0;
    int right = array.length - 1;

    while (left <= right) {
      int s = array[left] + array[right];

      if (s == targetSum) {
        return new int[]{array[left], array[right]};
      } else if (s < targetSum) {
        left++;
      } else if (s > targetSum) {
        right--;
      }
    }
    return new int[]{-1, -1};
  }
}

Complexity Analysis

Time complexity: O(N log N), Sorting takes O(N log N), and running through a loop takes O(n) time. So overall time complexity is O(N log N).

Space Complexity: O(1) We didn’t flood any data onto memory. We used variables to store temporary data which is arbitary.