CodeChef - Small Factorials
Small factorials problem from CodeChef.

Problem
This problem basically asks you to calculate the factorial of a number up to 100. Now, I guess most of you know what a “factorial” is. For those who don’t, the factorial of a number N is 1*2*…*N. This problem would be very simple, had it not been for the maximum value of N. The structure of the problem is such that it asks the user to take the number of test cases as the first input. Then ‘t’ integers follow where ‘t’ is the number of test cases which was given as input previously.
For every integer here, we have to calculate the factorial. This is very simple in languages like Python or Java which have built-in support for big integer types. It proves to be a hassle for people using C / C++ or languages that do not have a built-in big integer type. Let’s think about how we can store the result.
Now, the maximum number that we can store in an unsigned 32-bit integer is 2 ^ 32 – 1, and in an unsigned 64-bit integer is 2 ^ 64 – 1. Something like 100! (‘!’ is the notation for factorial) has over 150 decimal digits. The data types mentioned earlier can store numbers having at most 9 and 19 decimal digits respectively. So, we need to find a way to store the 150+ digits that we will get as the answer. The simplest data structure that we can use is an integer array of size of about 200 to be on the safe side.
In the simplest form, let us store one decimal digit per array index. So, if the number is say 120, then the array will have the numbers as follows:
Say a[200] is how we declare the array, then
a[0] = 0
a[1] = 2
a[2] = 1
The least significant digit is stored in the lowest index 0. The next one is in index 1 and so on. Along with the array, we need an integer specifying the total number of digits in the array at the given moment. Let this number be m. Initially, a[0] will be 1 and the value m will be 1 specifying that we have just one digit in the array.
Let’s take a simple example first. Consider that the array has some value like 45 and we need to multiply it with a value of 37. This can be done in the following way.
The array will be:
a[0] = 5
a[1] = 4
and the value of m will be 2 specifying that there are 2 digits in the array currently.
Now, multiply this array by the value 37. We start off from index 0 of the array to index 1. At every iteration, we calculate 37 * a[index]. We also maintain a temporary variable called temp which is initialized to 0. Now, at every step, we calculate x = a[index] * 37 + temp. The new value of a[index] will be x % 10 and the new value of temp will be temp / 10. We are simply carrying out multiplication the way it is usually carried out. So, for the current situation, the iterations will be something like this.
Initialize temp = 0
Iteration 1 :
array = (5, 4)
temp = 0
index = 0, a[index] = 5
x = a[index] * 37 + temp = 5 * 37 + 0 = 185.
the new value of a[index] = 185 % 10 which is 5and the new value of temp is 185 / 10 which is 18
Iteration 2 :
array : (5, 4)
temp = 18
index = 1, a[index] = 4
x = a[index] * 37 + temp = 4 * 37 + 18 = 166.
the new value of a[index] = 166 %10 which is 6 and the new value of temp is 166 / 10 which is 16
We have finished 2 iterations and this is the value of m, the array size at the moment. The required number of iterations is now over, but the value of temp is still greater than 0. This means that the current value of temp will be incorporated into the array. For that, we keep appending the last digit of temp to the array and divide temp by 10 till temp becomes 0. So, we will get something like
Iteration 1 :
temp = 16 , array = (5, 6)
So, we add 16 % 10 to the array so that the array becomes (5, 6, 6) and we divide temp by 10 so that temp becomes 1. We update the value of m to m + 1 that is m = 3
Iteration 2 :
temp = 1, array = (5, 6, 6)
Now, we add 1 % 10 to the array, so the array becomes (5, 6, 6, 1) and we divide temp by 10 so that temp becomes 0. We update the value of m to m + 1 that is m = 4
The value of temp is now 0 and our multiplication is now over. The final array we get is (5, 6, 6, 1)
Voila, which we have the answer to 45 * 37 in our array with the Least significant digit in the 0th position.
For finding the factorial, we need to carry out this exact multiplication operation at every step as we loop from 1 to N. At the end of the Nth iteration, our array will contain
the answer and the value of m will be the number of digits in the answer. We can then just print the array from the Most significant digit to the least for the answer.
The basic flow of the program will be as below :
StartTake in the number of test cases while there is a test case remaining to be handled Take in the number whose factorial is to be found, let it be N Initialize the array's 0th index to 1 and m to 1 Initialize i to 1 While i is less than or equal to N Carry out the multiplication of the array with i as shown above. Print the contents of the array starting from the most significant digit and ending with the least significant digit. Stop
Certain improvements can be made to the above-mentioned method. We are storing only one digit per array index, We can store more than 1 digit per index so that the number of computations is reduced. The method to do that is the same as above. We leave it to the reader as an exercise.
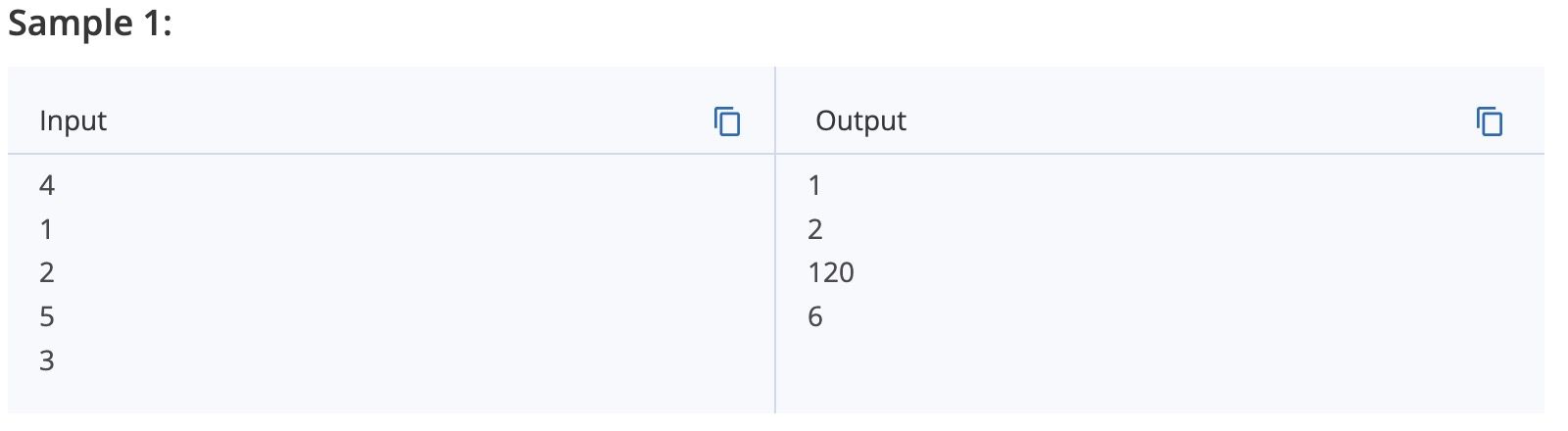
Input
An integer t, 1<=t<=100, denoting the number of test cases, followed by t lines, each containing a single integer n, 1<=n<=100.
Output
For each integer n given at input, display a line with the value of n!
Solution in Java:
import java.util.*;
import java.lang.*;
import java.math.*;
class Codechef
{
public static void main (String[] args)
{
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(t-- > 0)
{
int n = sc.nextInt();
BigInteger fact = new BigInteger("1");
for(int i = 2; i <= n; i++)
{
fact = fact.multiply(BigInteger.valueOf(i));
}
System.out.println(fact);
}
sc.close();
}
}



